Intro
Each section has code examples (see "Code Examples") implementing the corresponding algorithm, all of which (plus more not covered in this blog post - if interested) can be found at my GitHub repo: https://github.com/MattCrook/algorithms-practice. The code examples consist of simply going through and explaining the algorithm and its implementation, as well as "challenges" (denoted by "Challenge" in the link title) which are coding problems structured in what you'd commonly see in interviews, which implement the specific algorithm.
- Space and Time Complexity
- Stacks
- Queues
- Graph Traversal
- Binary Search Algorithm
- LinkedList
- HashMap
- Two Sum and Three Sum (Two Pointer/ Three Pointer)
- Fibonacci Sequence
- Circular Buffer
- Pascal's Triangle
- Valid Palindrome
- String Manipulation
- Sorting Algorithms
- Array/ List Manipulation Algorithms
- Simple Searching Algorithms
- Various Counting Algorithms
- Fizzbuzz
- Extra Challenges/ Examples
Space and Time Complexity
Before we start talking about algorithms, it is important to discuss their purpose and how it relates to space and time complexity. In computer science algorithms, there is something called the “Big O Notation” (See chart below). It primarily looks at how many operations a sorting algorithm takes to completely sort a very large collection of data. This is a measure of efficiency and is how you can directly compare one algorithm to another. All algorithms can be measured by this, in Time Complexity and Space Complexity.
It is important to note that there is no single algorithm that is fastest in all cases, as data can be input into a program in all manners of states. And the approaches of each algorithm will have a best case and worst case scenario where they perform at their best or worst. So it is the programmers job (and your job in an interview for example) to leverage the best implementation to find the desired solution.
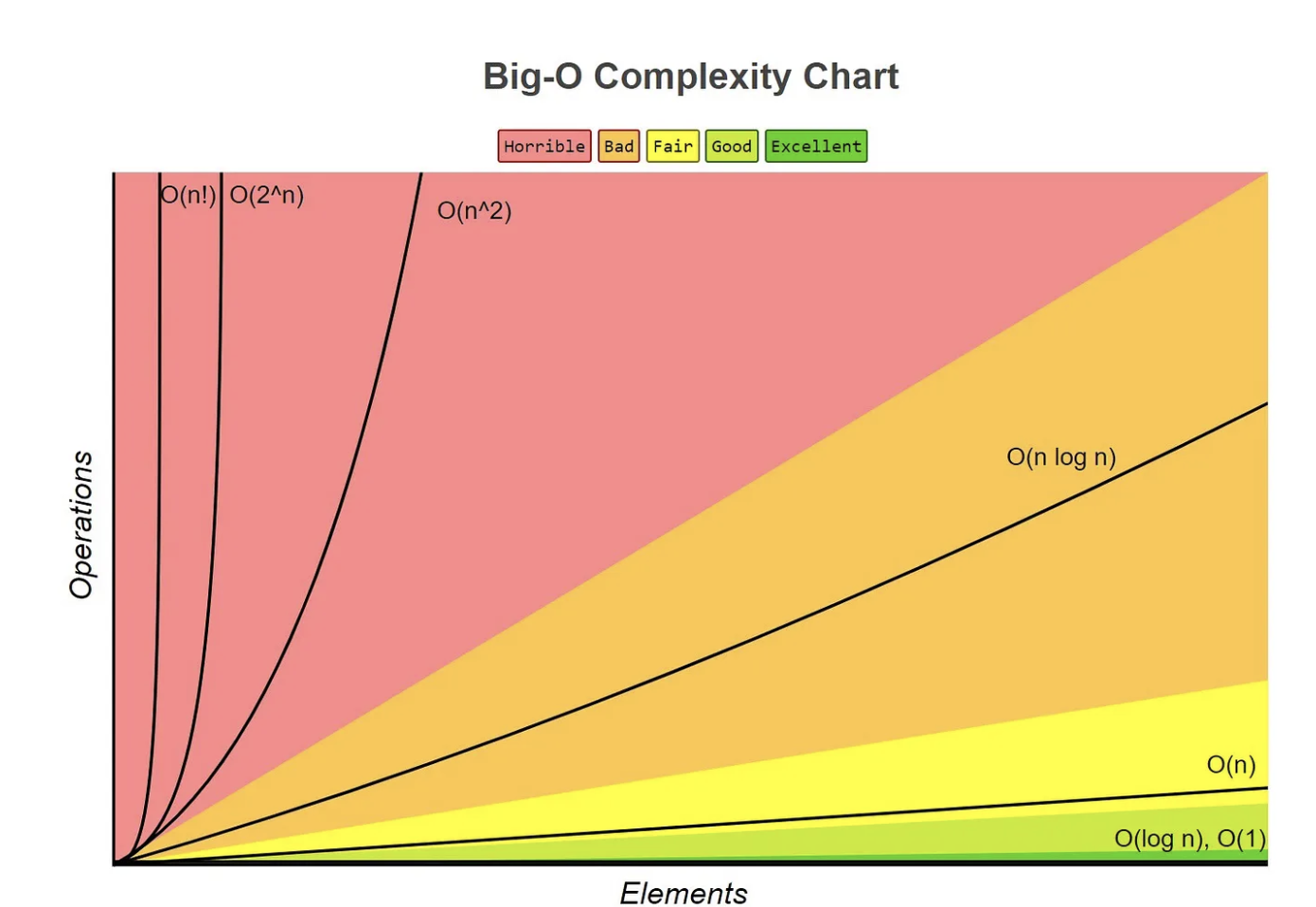
Time complexity is concerned with how the running time of an algorithm or function grows as the size of the input increases. We analyze the time complexity by counting the number of basic operations or steps the function performs, and then express that in Big-O notation. The Big-O notation is used to express the upper bound of time complexity, and after counting operations, express the complexity in terms of the most significant term. For example: a single loop over n elements results in O(n), a nested loop over n elements results in O(n²), and a recursive function with halving input size results in O(log n).
Space complexity is concerned with how much memory (space) an algorithm uses as a function of the input size. This includes the space used by variables, data structures, function call stacks, and so on. If the function is recursive, space complexity can be affected by the call stack. Each recursive call adds a new layer to the stack, and in some cases, this contributes to space complexity. And just like time complexity, space complexity is often simplified to Big-O notation.
Stacks
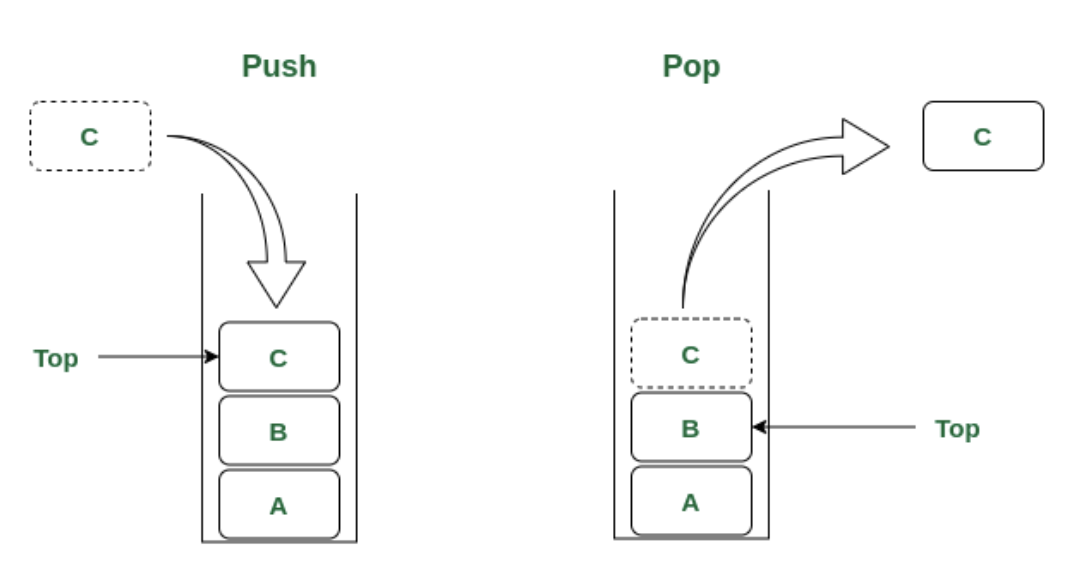
The stack data structure is precisely what it sounds like: a stack of data. In certain types of scenarios, it can be favorable to store data in a stack rather than in an array. A stack uses LIFO (last-in, first- out) ordering. That is, as in a stack of dinner plates. The most recent item added to the stack is the first item to be removed.
Unlike an array, a stack doesn't offer a consent-constant time access to the ith item. However, it does allow constant-time adds and removes as it doesn't require shifting elements around. One case where stacks are often useful is in certain recursive algorithms. Sometimes you need to push temporary data onto a stack as you recurse, but then remove them as you backtrack (for example, because the recursive check failed). A stack offers an intuitive way to do this. A stack can also be used to implement a recursive algorithm iteratively.
Queues
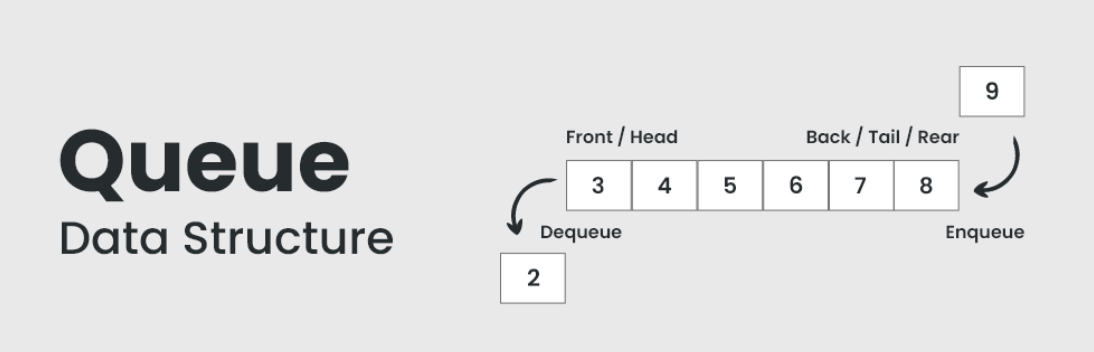
A Queue implements FIFO (first-in, first-out) ordering. As in a line or queue at a ticket stand, items are removed from the data structure in the same order that they are added. A queue can also be implemented with a Linked List. In fact, they are essentially the same thing as long as items are added and removed from opposite sides.
One thing to note with a queue is, it is especially easy to mess up the updating of the first and last nodes. One place are often used in breadth-first search, or an implementing a cache. In breadth-first search for example, we use a queue to store a list of nodes that we need to process. Each time we process a node, we add its adjacent nodes to the back of the queue. This allows us to process nodes in the order in which they are viewed.
Graphs
Graph Search and Graph Traversal
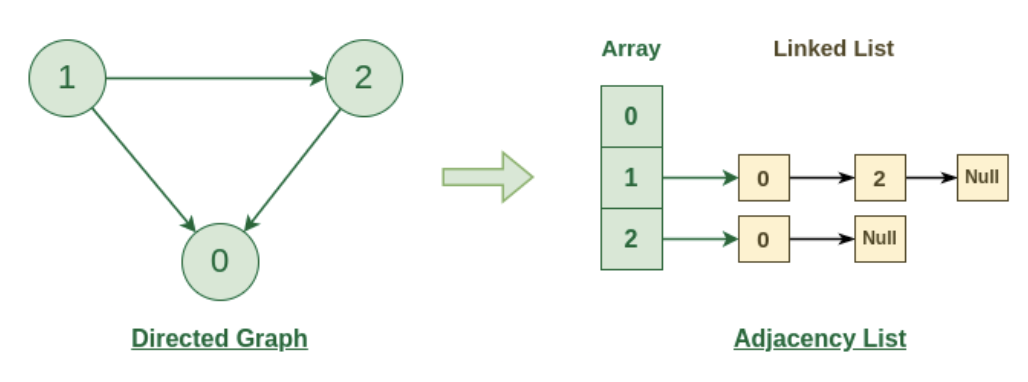
Adjacency List
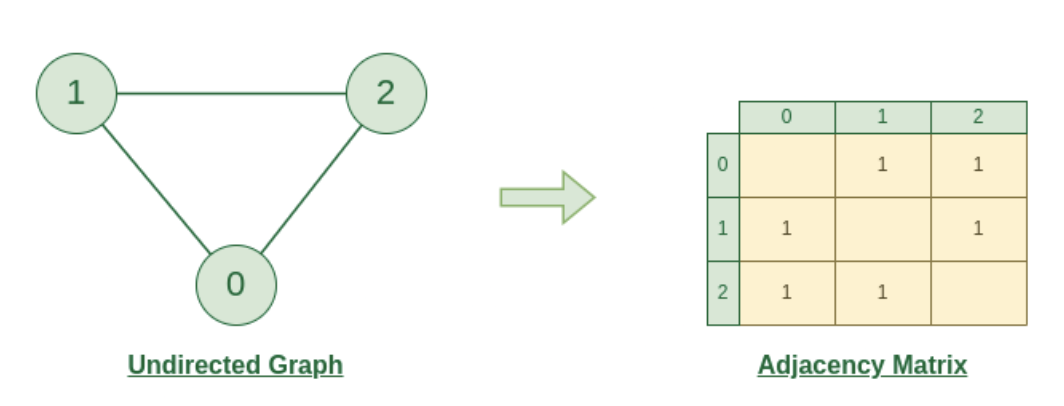
An adjacency list is the most common common way to represent a graph. Every vertex (or node) stores a list of adjacent vertices. In an undirected graph, an edge like (a, b) would be stored twice: once in a's adjacent vertices, and once in b's adjacent vertices.
Adjacency Matrix
An adjacency matrix is N x N boolean matrix (where N is the number of nodes), where a true value at matrix[i][j] indicates an edge from node i to node j. You can also use an integer matrix with 0's and 1's. In an undirected graph, an adjacency matrix will be symmetric. In a directed graph, it will not necessarily be. The graph algorithms that are used on adjacency lists can be performed with adjacency matrices, but they may be somewhat less efficient. In the adjacency list representation, you can easily iterate through the neighbors of a node. In the adjacency matrix representation, you will need to iterate through all the nodes to identify a node's neighbors.
Algorithms
Two common ways to search a graph are:
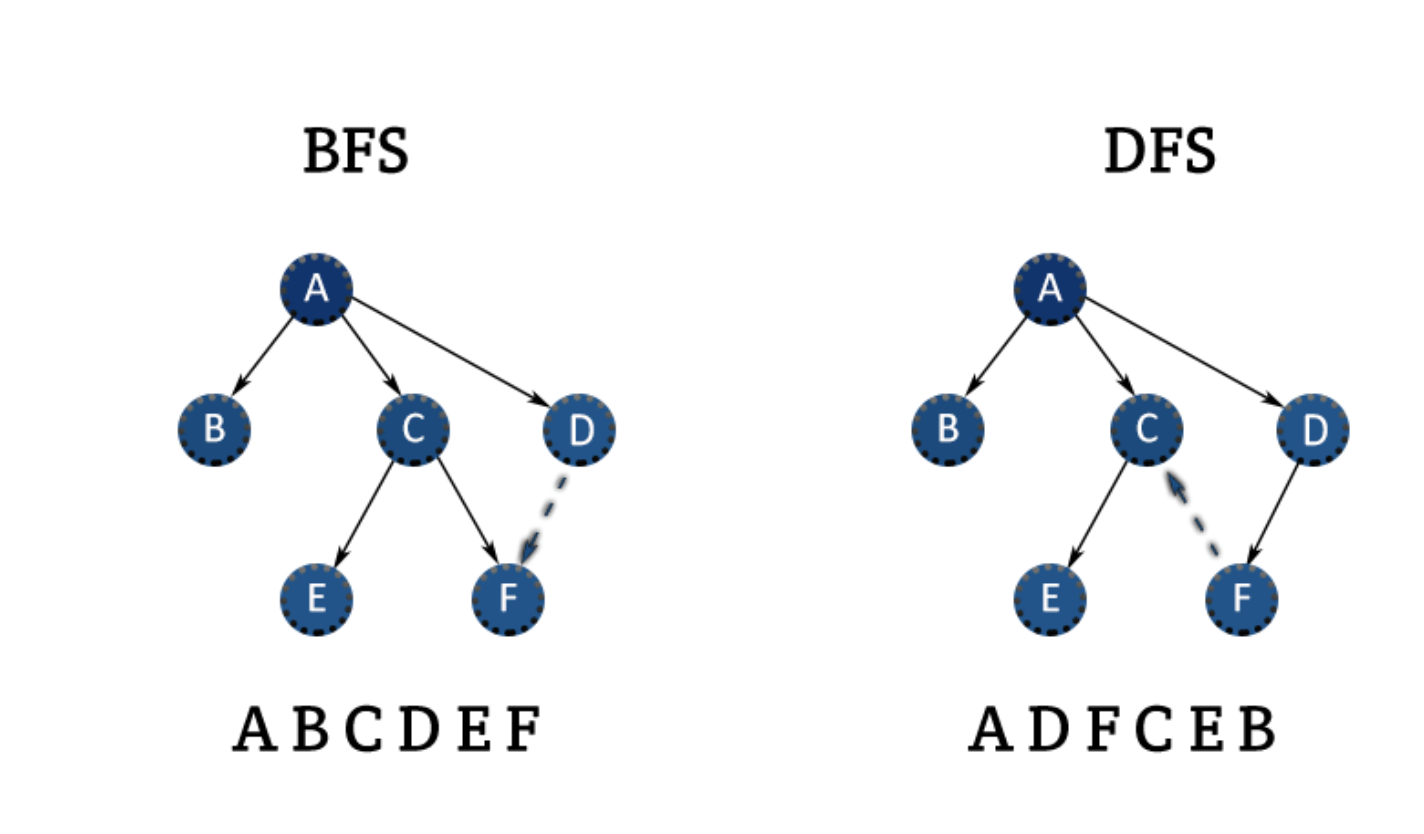
In Depth-First Search (DFS), we start at the root (or another arbitrarily selected node) and explore each branch completely before moving onto the next branch. That is, we go deep first (hence the name depth- first search) before we go wide. In DFS we visit a node `a`, and then iterate through each of `a's` neighbors. When visiting a node `b` that is a neighbor of `a`, we visit all of `b's` neighbors before going onto `a's` other neighbors. That is, `a` exhaustively searches `b's` branch before any of its other neighbors. The difference in this algorithm for a graph, is that we must check if the node has been visited. If we do not, we risk getting stuck in an infinite loop.
In Breath-First Search, we start at the root (or another arbitrarily selected node) and explore each neighbor before going onto any of their children. That is, we go wide (hence the name breath- first) before we go deep. BFS is a bit less intuitive, and it is easy to struggle with the implementation unless you are already familiar with it. The main tripping point is the false assumption that BFS is recursive. It is not, it uses a queue. In BFS, node a visits each of a's neighbors before visiting any of their neighbors. You can think of this as searching level by level out from a. An iterative solution involving a queue usually works best.
Breath-First Search (BFS) and Depth-First Search (DFS) tend to be used in different scenarios.- DFS is often preferred if we want to visit every node in the graph. Both will work fine but depth first search is a bit simpler in this case.
- However, if we want to find the shortest path or just any path between (2) nodes, BFS is generally better.
- Graph Traversal I (Python)
- Graph Traversal I (Javascript)
- Graph Traversal II (Python)
- Graph Traversal II (Javascript)
- Graph Traversal III (Python)
- Graph Traversal III (Javascript)
- Adjacency Matrix (Graph Traversal Challenge) (Javascript)
- DFS / BFS Surrounded Regions (Challenge) (Python)
- Simple Adjacency List (Python)
- Additional Graph Traversal Example - Itinerary (Python)
- Find Diagonal Sum Of Matrix
Binary Search
When we think of searching algorithms, we generally think of a binary search. In a binary search, we look for an element X in a sorted array by first comparing X to the midpoint of the array. If X is less than the midpoint, then we search the left half of the array. If X is greater than the midpoint, then we searched the right half of the array. We then repeat this process treating the left and right has a sub arrays. Again, we compare X to the midpoint of this sub array, and then search either it's left or right side. We repeat this process until either we find X, or the sub array has a size of 0.
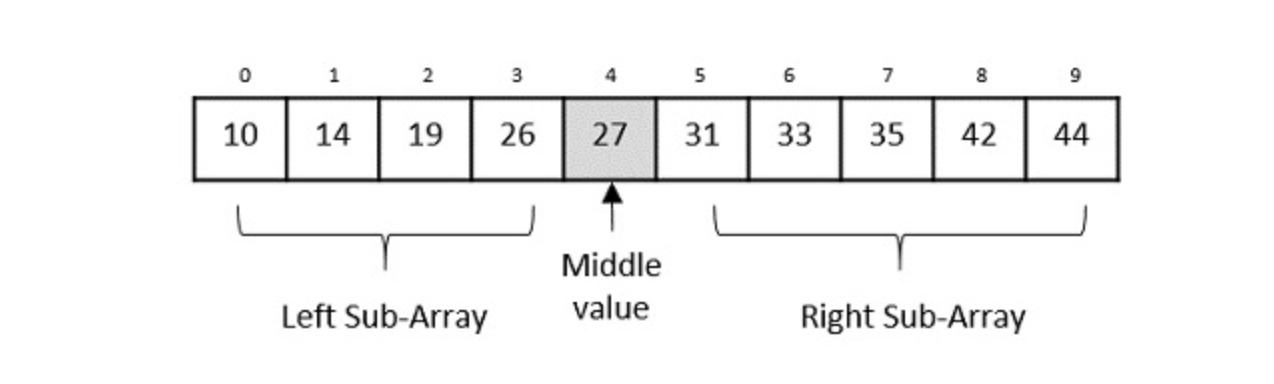
There are two main ways to perform this type of search. One using a while loop (similar to a queue algorithm), and another using recursion. There are code examples of both provided below. Important to note, though this algorithm may seem somewhat simple on the surface, getting the details correct (especially the plus and minuses (see code examples) when deciding on which direction of a sub array to search next) is more tricky than one might think. (In my opinion).
- Binary Search (Python)
- Binary Search (Javascript)
- Binary Search II (Python)
- Binary Search II (Javascript)
- BFS and DFS Binary Search (Javascript)
- Convert Array To Binary Search Tree (Python)
- Convert Sorted Array To Binary Search Tree (Javascript)
- Find Max Depth of Binary Search Tree (Python)
Linked Lists
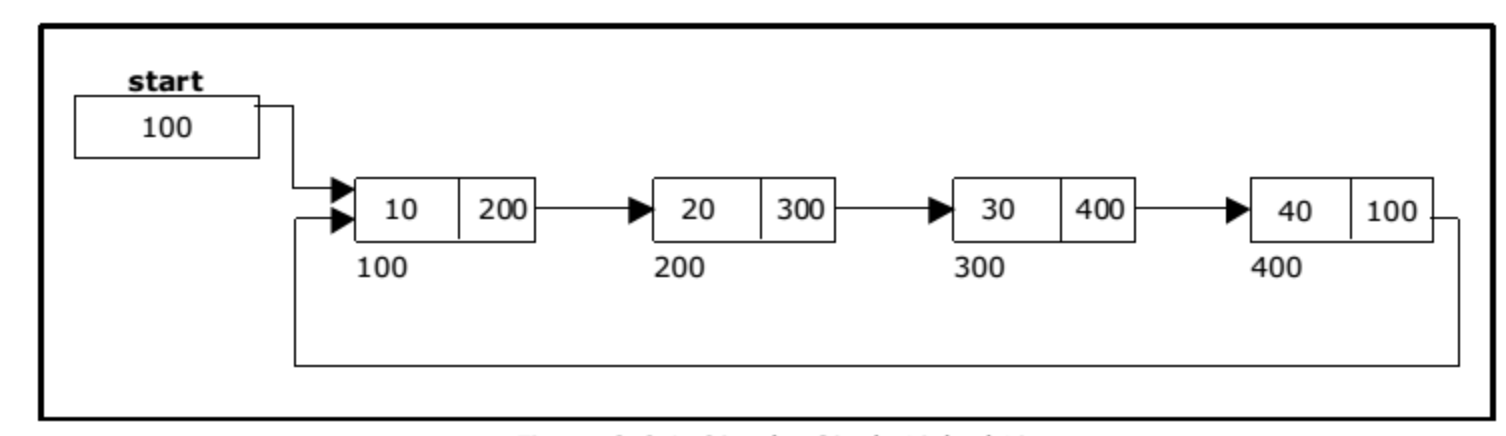
A Linked List is a data structure that represents a sequence of nodes. In a singly Linked List, each Node points to the next Node in the Linked List. A doubly Linked List gives each Node pointers to both the next Node and the previous Node.
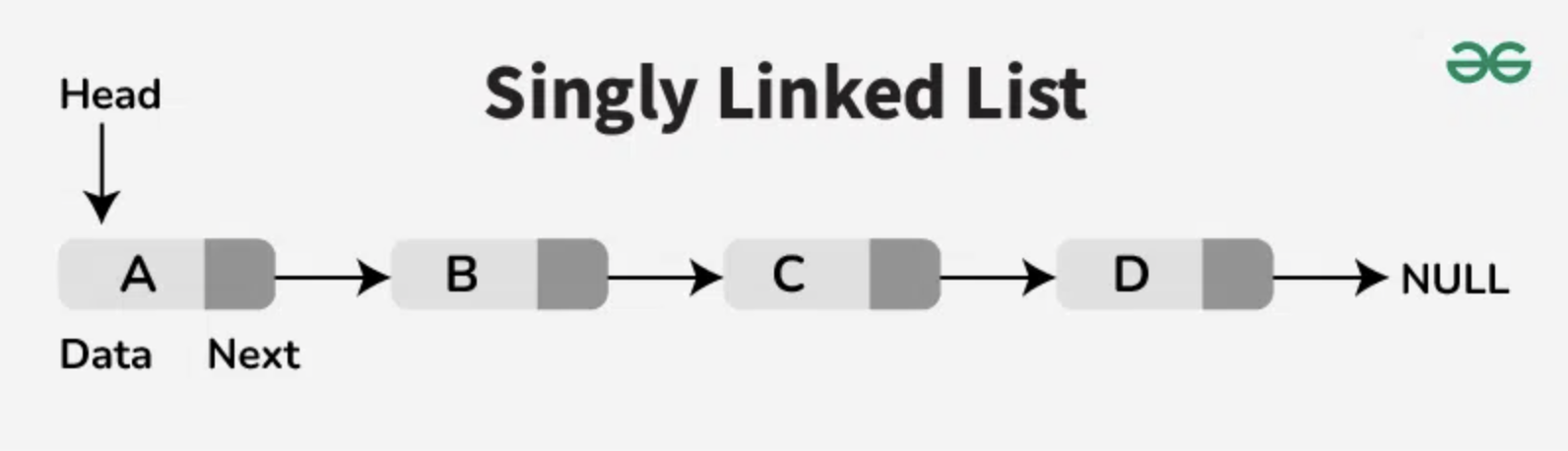
Unlike an array, a linked list does not provide constant time access to a particular index within the list. This means that if you'd like to find the Kth element in the list, you will need to iterate through K elements. The benefit of a Linked List is that you can add and remove items from the beginning of the list and constant time. For specific applications, this can be useful.
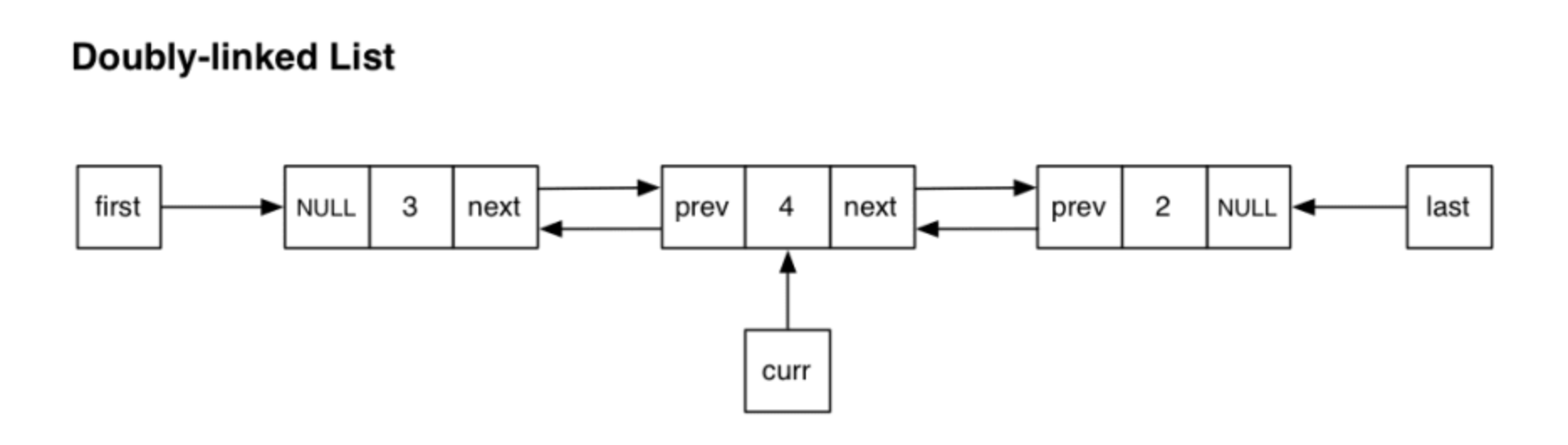
A circular Linked List connects the last Node back to the first Node.
- LinkedList Code Example (Javascript)
- LinkedList Code Example (Python)
- Doubly LinkedList Code Example (Javascript)
- Add Two Numbers, Return Sum of LinkedList (Challenge) (Python)
HashMap
A HashMap or Hash Table is a data structure that maps keys to values for highly efficient lookups. There are a number of ways of implementing this.
A simple implementation is we can use an array of linked lists, and a hash code function. To insert a key which might be a string or essentially any other data type and value, we first compute the key's hash code. Then, map the hash code to an index in the array. At this index, there is a linked list of keys and values. Store the key and value in this index. (We must use a linked list because of collisions.) Then, to retrieve the value pair by its key, we repeat the process: compute the hash code from the key, then compute the index from the hash code, then search through the linked list for the value with this key.
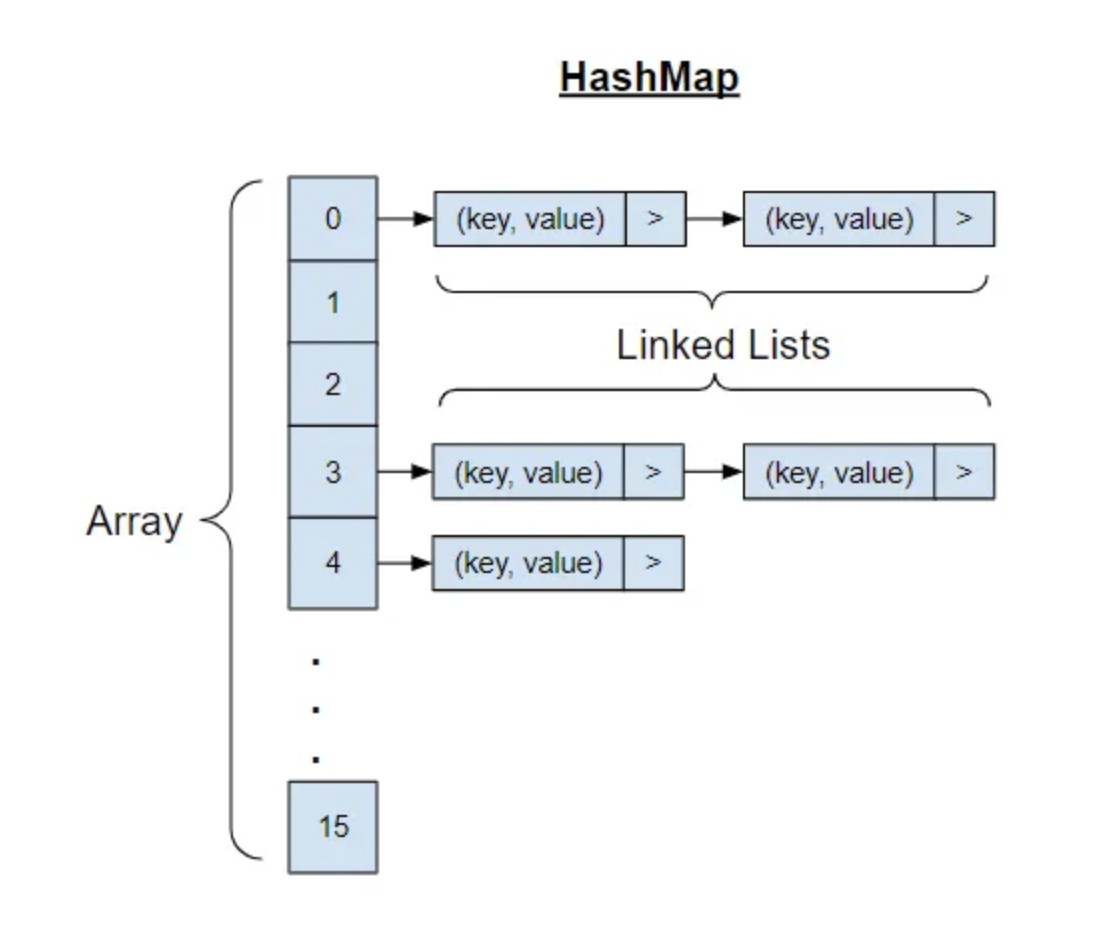
Basically, it’s an array of linked list. Ideally, each item in the array is a linked list of just 1 node. So you can get O(1) complexity to perform get and put by calculating the index of the array by hashing the key of the hashmap, and get the single item in the linked list. However, because hash function doesn’t have to create a unique hash code for different values, when more than 1 key have the same hash code, they are added to the linked list. So, to get to the correct key, you’ll need to traverse the linked list and compare the key one by one, thus resulting in a complexity of O(n) for those keys with the same hash code.
Alternatively, we can implement a look up system with a balanced binary search tree. This gives us O(log n) lookup time. The advantage of this is potentially using less space since, we no longer allocate a large array. We can also iterate through the keys in order; which can also be useful sometimes.
- Two Sum Algorithm Using HashTable/ HashMap (Javascript)
- Two Sum Algorithm Using HashTable/ HashMap (Python)
- Additional Simple HashMap Code Example (Two Sum Algorithm) (Challenge) (Javascript)
- Additional Simple HashMap Code Example (Two Sum Algorithm) (Challenge) (Python)
Two Sum and Three Sum (Two Pointer/ Three Pointer)
One of the many popular algorithms is the Two Sum Algorithm. Given an array of numbers and a stand alone number, return all combinations of numbers in the array that add up to the stand alone number. Although any approach that works is technically a solve, but Big O determines which is the best answer for your application.
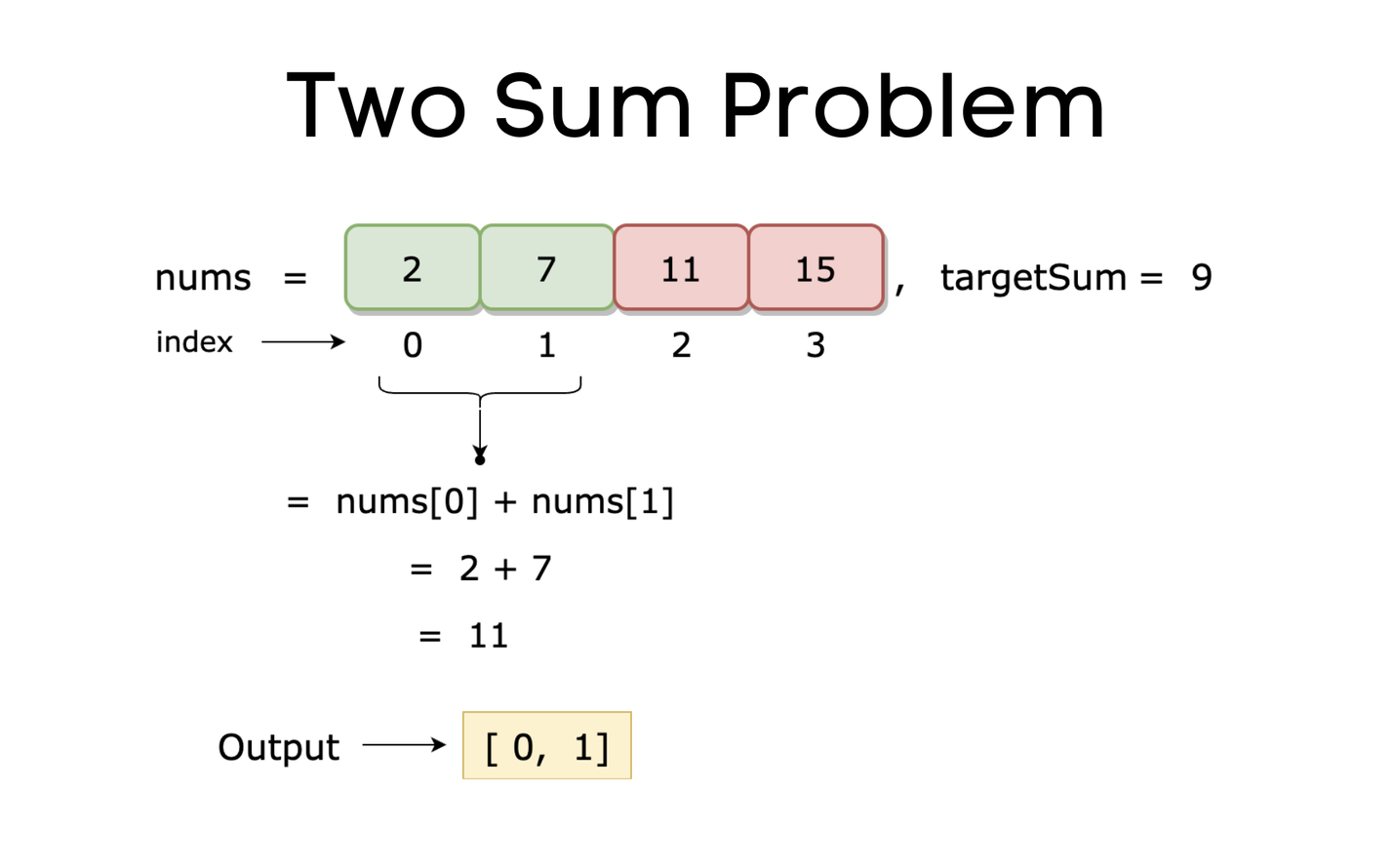
The two sum problem is a common interview question, and it is a variation of the subset sum problem. The challenge is to find all the pairs of two integers in an unsorted array that sum up to a given Sum.
The Three Sum problem involves finding unique triplets of numbers in an array that sum up to a given target. Solve it efficiently by building on top of the Two Sum problem and applying sorting and hashing approaches. This problem is a continuation of "Two Sum" in which the premise is very similar. As with that problem, for Three Sum there are naive, combination-driven approaches as well as more-efficient approaches.
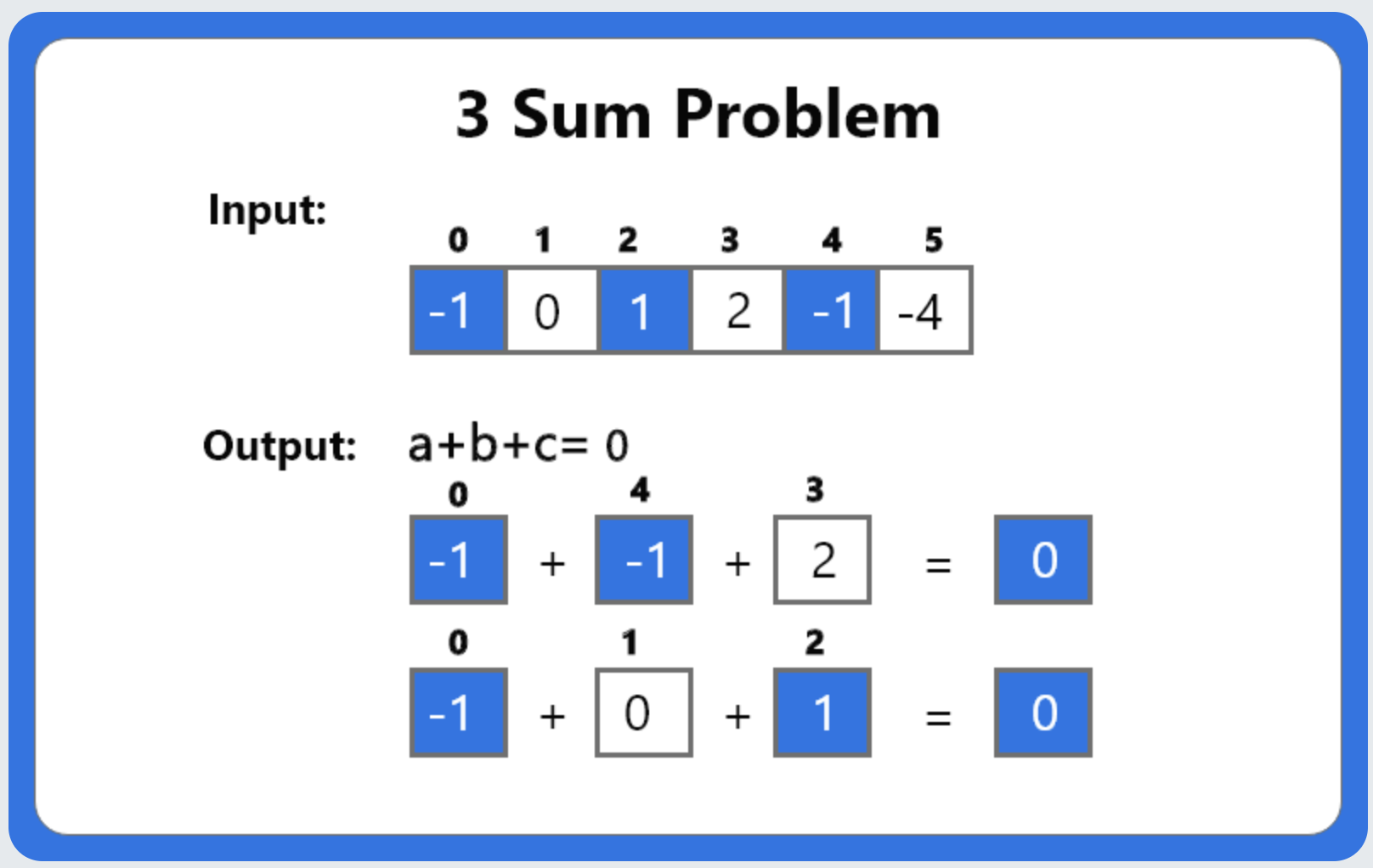
- Two Sum (Javascript)
- Two Sum (Python)
- Simple Two Sum (Challenge) (Python)
- Simple Two Sum (Challenge) (Javascript)
- Two Sum II (Challenge) (Python)
- Two Sum II (Challenge) (Javascript)
- Three Sum (Javascript)
- Three Sum (Python)
- Three Sum (Challenge) (Javascript)
- Three Sum (Challenge) (Python)
Fibonacci Sequence
The Fibonacci sequence is the series of numbers where each number is the sum of the two preceding numbers. It starts with 0 and is followed by 1.
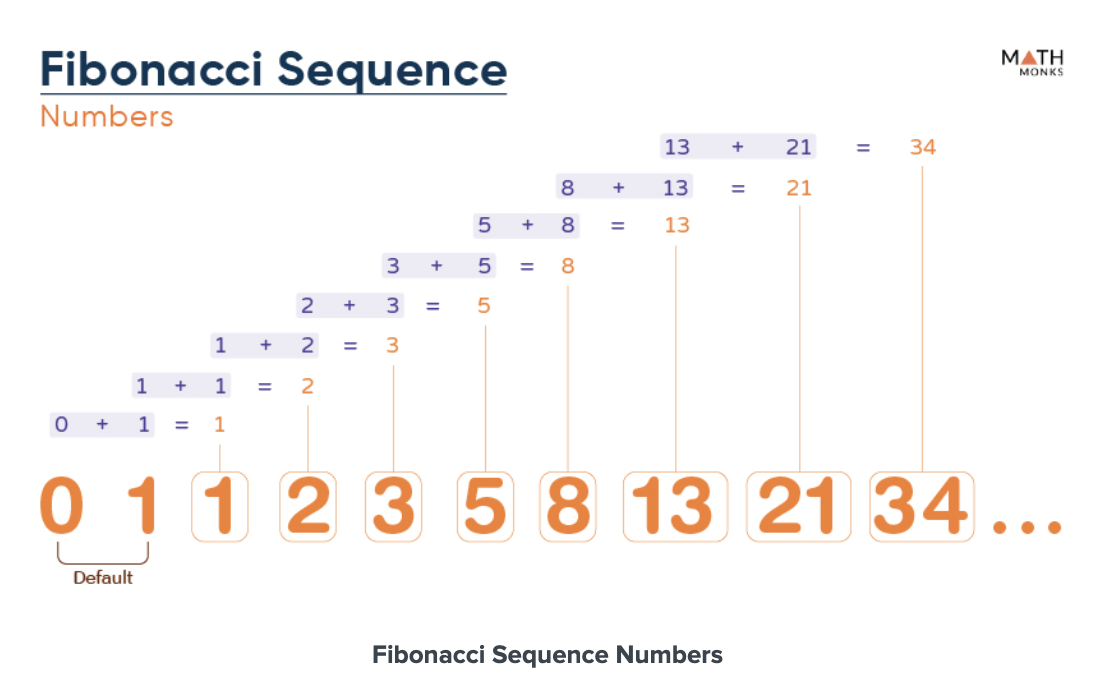
The numbers in this sequence, known as the Fibonacci numbers, are denoted by F(n).

- Fibonacci Sequence (Using Iterative and Recursive Approaches) (Python)
- Fibonacci Using Memoization (Javascript)
Circular Buffer
A a circular buffer (or circular queue, cyclic buffer or ring buffer) is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end.
This structure lends itself easily to buffering data streams.
The useful property of a circular buffer is that it does not need to have its elements shuffled around when one is consumed.
(If a non-circular buffer were used then it would be necessary to shift all elements when one is consumed.)
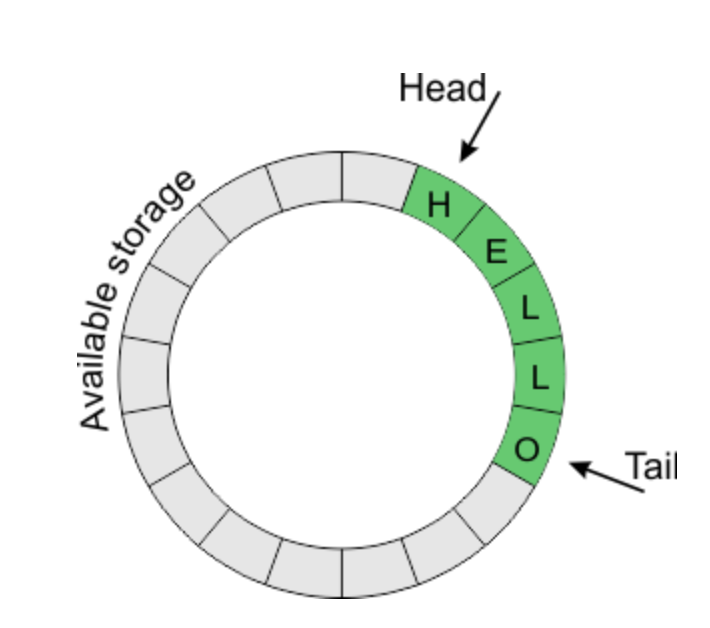
In other words, the circular buffer is well-suited as a FIFO (first in, first out) buffer while a standard, non-circular buffer is well suited as a LIFO (last in, first out) buffer. Circular buffering makes a good implementation strategy for a queue that has fixed maximum size. Should a maximum size be adopted for a queue, then a circular buffer is a completely ideal implementation; all queue operations are constant time. However, expanding a circular buffer requires shifting memory, which is comparatively costly. For arbitrarily expanding queues, a linked list approach may be preferred instead.
- Circular Buffer More Detailed Code Example (Javascript)
- Circular Buffer More Detailed Code Example (TypeScript)
- Additional Circular Buffer Solutions/ Implementations (Javascript)
Pascal's Triangle
In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. The rows of Pascal's triangle are conventionally enumerated starting with row n=0 at the top (the 0th row). The entries in each row are numbered from the left beginning with k=0 and are usually staggered relative to the numbers in the adjacent rows.
The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in row 3 are added to produce the number 4 in row 4.

Valid Palindrome
A phrase is a palindrome if, after converting all uppercase letters into lowercase letters and removing all non-alphanumeric characters, it reads the same forward and backward. Alphanumeric characters include letters and numbers.
String Manipulation
- Longest Common Prefix: String Amongst an Array of Strings (Challenge) (Python)
- Longest Common Prefix: String Amongst an Array of Strings (Challenge) (Javascript)
- Reverse a String (Challenge) (Python)
- Convert Sentence to Array of Strings (Challenge) (Javascript)
- Various String Manipulation Functions (Python)
- Buy and Sell Stock (Challenge) (Python)
- Buy and Sell Stock (Challenge) (Javascript)
Sorting Algorithms
Merge Sort
Merge Sort is a divide-and-conquer algorithm. It works by dividing the array into two halves, sorting each half recursively, and then merging the sorted halves. Merge Sort algorithm splits the array and recursively sorts the halves, an alternative approach can be to implement it iteratively using bottom-up merging. This avoids recursion and uses a non-recursive approach to merge sub-arrays in a bottom-up manner.
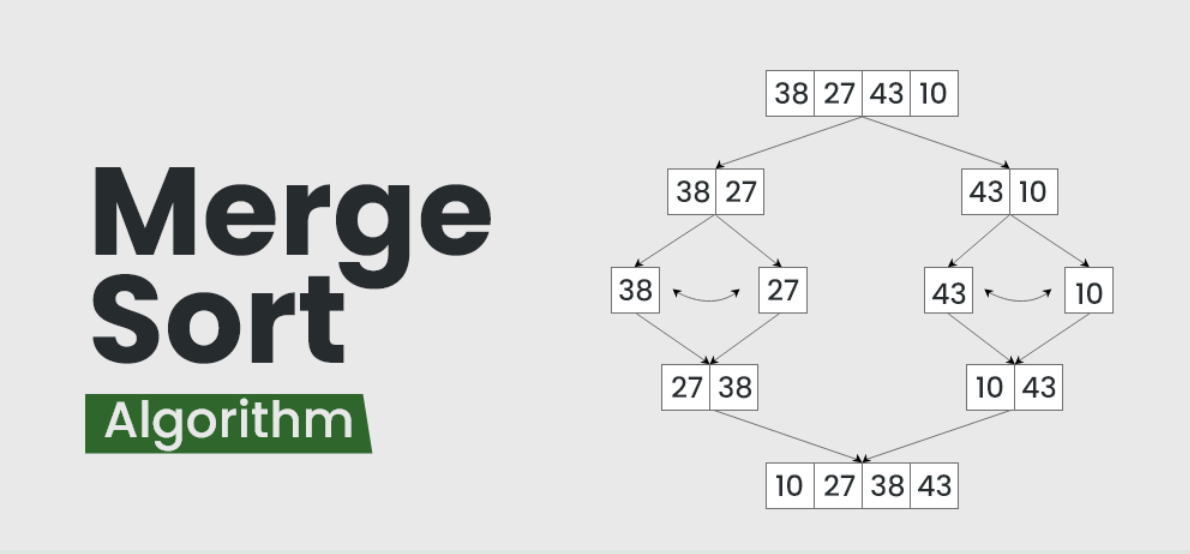
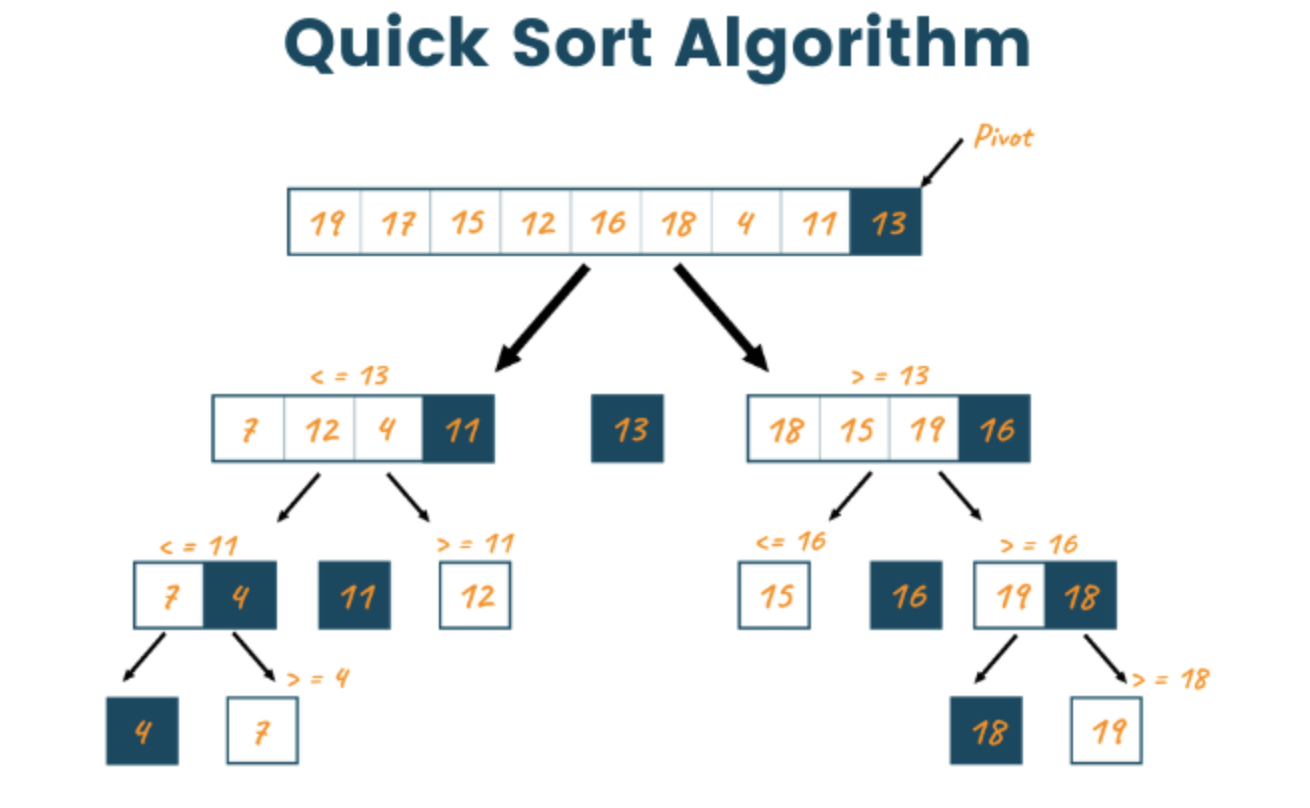
Quick Sort
Quick Sort is another divide-and-conquer algorithm. It works by selecting a pivot element from the array and partitioning the other elements into two sub-arrays: those less than the pivot and those greater than the pivot. These sub-arrays are then sorted recursively. Quick Sort is generally faster than other O(n log n) algorithms (like Merge Sort) in practice due to smaller constant factors and better cache performance. The worst-case time complexity of O(n²) can be avoided with random pivot selection or using techniques like median-of-three to choose the pivot. Examples shown include a simple example of Quick Sort using a not in place sorting method, in-place sorting method with Lomuto Partition Scheme, and in-place method using Hoare's Partition Scheme. Important to note there are many other methods, such as random pivot selection or using techniques like median-of-three as mentioned previously.
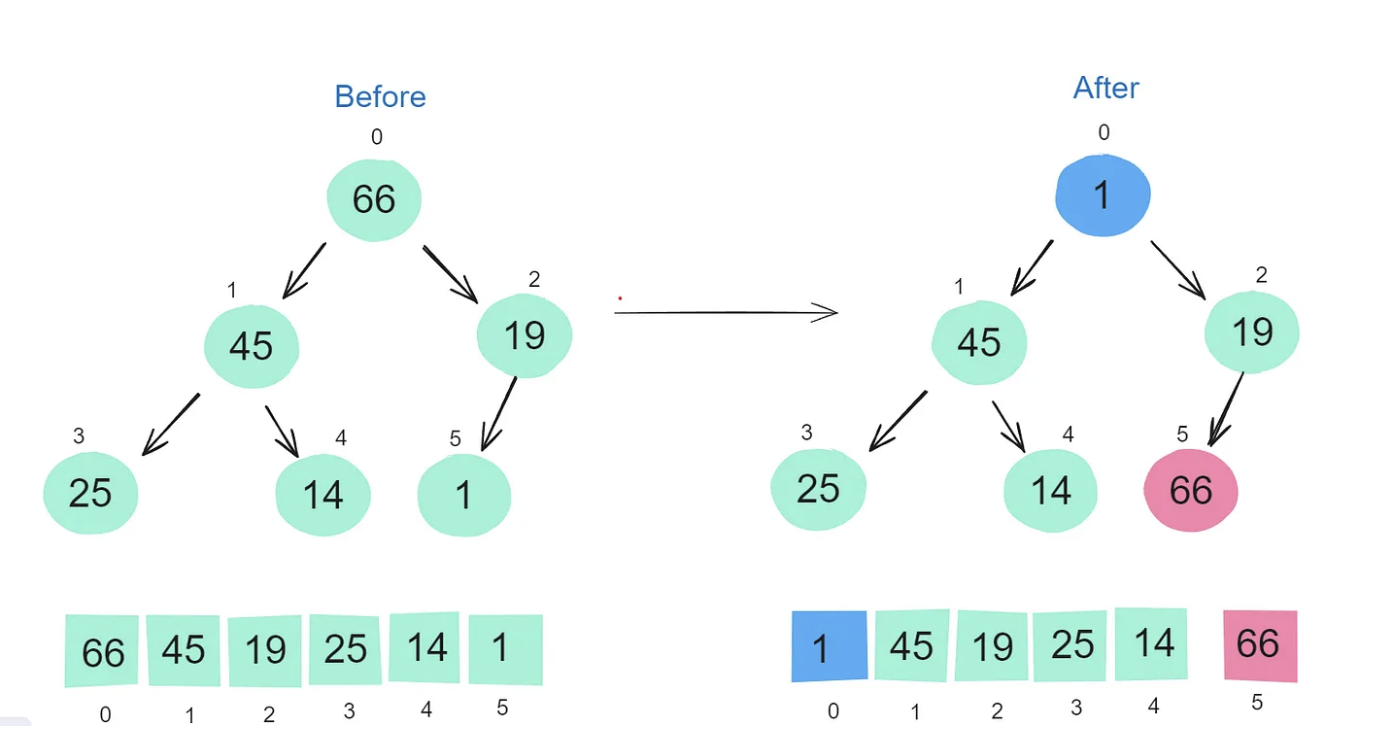
Heap Sort
Heap Sort is a comparison-based sorting algorithm that takes advantage of a binary heap data structure to efficiently sort an array or list. It works by first transforming the list into a max-heap or a min-heap, and then repeatedly extracting the largest (or smallest) element to build the sorted array. Heap Sort is a very efficient sorting algorithm with a guaranteed time complexity of O(n log n). It is an in-place, non-stable sorting algorithm that uses a binary heap to efficiently find the largest element and place it in its correct position. It is particularly useful in situations where space complexity is a critical factor, but the lack of stability might be a downside for some use cases.
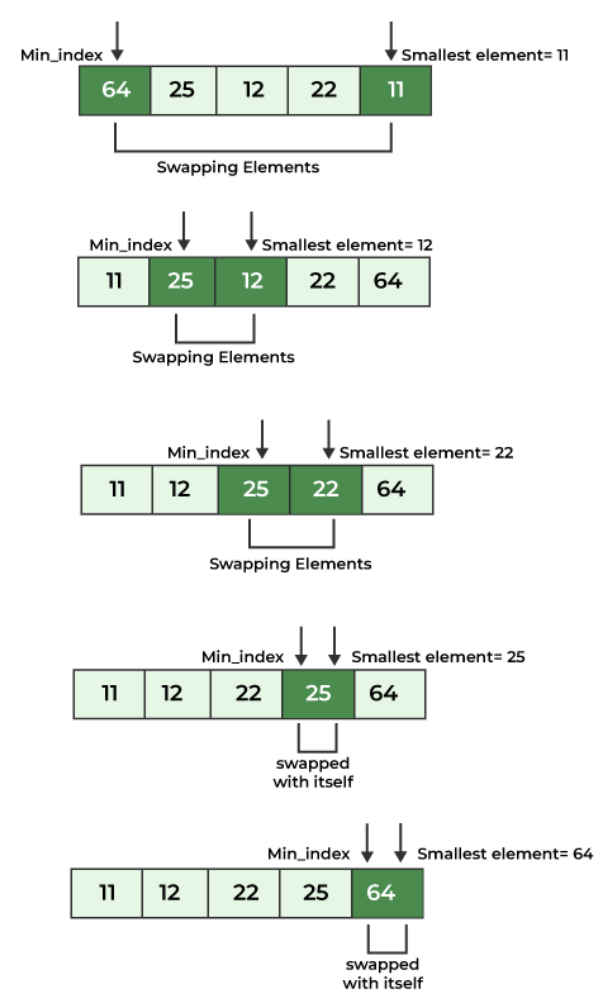
Selection Sort
Selection Sort is a simple comparison-based sorting algorithm that works by repeatedly finding the minimum (or maximum) element from the unsorted part of the list and swapping it with the first unsorted element. It works by reducing the unsorted portion of the array step by step. It uses in-place sorting, meaning the algorithm sorts the array in place without needing extra memory, it is non-stable meaning that it may change the relative order of equal elements, and the algorithm always performs O(n²) comparisons, regardless of the input's order.
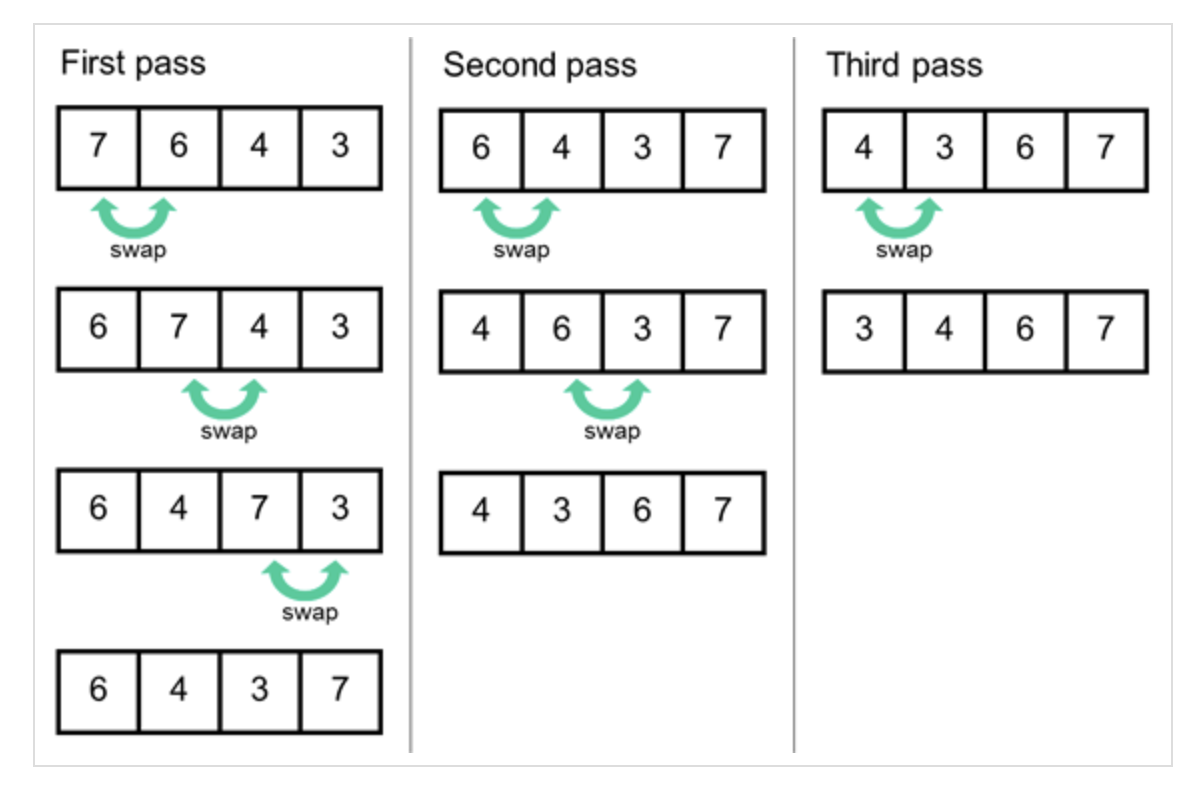
Bubble Sort
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list to be sorted, and compares each pair of adjacent items and swaps them if they are in the wrong order (ascending or descending arrangement). The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. Bubble Sort is an in-place sorting algorithm, and only requires a constant amount of additional memory regardless of the input size. While not the most efficient for large datasets, it's useful for small arrays or when you need a very simple sorting algorithm.
- Merge Sort (Javascript)
- Merge Sort (Python)
- Quick Sort (Javascript)
- Quick Sort (Python)
- Heap Sort (Javascript)
- Heap Sort (Python)
- Selection Sort (Javascript)
- Selection Sort (Python)
- Bubble Sort (Javascript)
Array/ List Manipulation Algorithms
The below array or list manipulation challenges and examples consist of fundamental techniques that (in addition to searching and sorting which has already been covered) require the performance of additional operations such as inserting, deleting, merging, and modifying elements within an array or list.
- Needle in Haystack (Occurrence First Index) (Challenge) (Python)
- Merge Sorted Array (Challenge) (Python)
- Search Insert Position (Challenge) (Python)
- Remove Element (Challenge) (Python)
- Remove Element (Challenge) (Python)
- Shuffle Array (Challenge) (Javascript)
- Shuffle List (Challenge) (Python)
- Find Largest Number In Array and Return Index (Javascript)
- Find Largest Number In List and Return Index (Python)
Simple Searching
Miscellaneous additional more simple searching algorithms and implementations. Some of these may not necessarily be "algorithms", but more of simply alternative approaches, varied methods, or distinct techniques to search various data structures.
- Find Name In a Phone Book: Simple Object Searching (Challenge) (Javascript)
- Find Odd Number In Given Array Of Numbers (Challenge) (Javascript)
- Find Smallest Number Out of 2 Integers (Challenge) (Javascript)
- Find Binary of Number (Challenge) (Javascript)
- Find Largest Number In List and Return Index (Python)
Various Counting Algorithms
Counting algorithms are algorithms used to determine the frequency or count of specific elements, typically in a collection or dataset. These algorithms can be used to track occurrences, frequencies, or even to help solve more complex problems like sorting or histogram generation. Below is a collection of "official" counting algorithms, such as:
- Counting Algorithms (Javascript)
- Count Distinct Ways To Climb To Top of Stairs (Challenge) (Javascript)
- Counting Occurrence in String (Javascript)
- Find All Odd Numbers in Given Array (Javascript)
- Make a Given Input Number Negative (Javascript)
- Find Length of Last Word (Javascript)
- Find Length of Last Word (Python)
- Find Smallest Number Of Two Integers (Javascript)
- Find Sum Of Range of Numbers In Array And Return It (Javascript)
Fizzbuzz
The FizzBuzz problem is a common coding task (often used in interviews or as a programming exercise). The task is to print the numbers from 1 to 100, but for multiples of 3, print "Fizz" instead of the number, and for multiples of 5, print "Buzz". For numbers that are multiples of both 3 and 5, print "FizzBuzz".
Extra Challenges / Examples
Random other examples, as well as coding problems I have been asked in technical interviews (the challenge may not be the exact problem I was asked, but I tried to recall to the best of my ability). These examples include a combination of coding challenges, as well as more DevOps type challenges / projects (i.e. standing up Infrastructure with Terraform).
- CallSigns (Challenge) (Python)
- Integer To Roman Numeral (Challenge) (Python)
- Integer To Roman Numeral (Challenge) (Javascript)
- Find H Index (Challenge) (Python)
- Find H Index (Challenge) (Javascript)
Written: November 2, 2024